Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
Find the coordinates of the image after the transformation.
|
|
|
1.
|
Translate 4 units right and 6 units up. 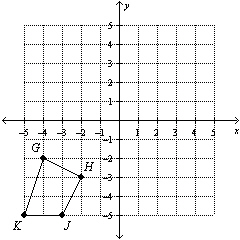 a. | G'(0, 4), H'(2, 3), J'(1, 1),
K'(–1, 1) | b. | G'(2, 2), H'(4, 1),
J'(3, –1), K'(1, –1) | c. | G'(–8, 4), H'(–6, 3), J'(–7,
1), K'(–9, 1) | d. | G'(0, –8), H'(2,
–9), J'(1, –11), K'(–1,
–11) |
|
|
|
2.
|
Reflect in the x-axis. 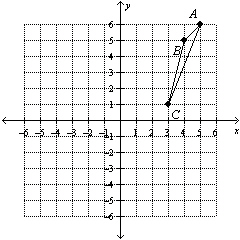 a. | A'(5, –6), B'(4, –5), C'(3,
–1) | c. | A'(–5, –6), B'(–4, –5),
C'(–3, –1) | b. | A'(–5, 6),
B'(–4, 5), C'(–3, 1) | d. | A'(5, 6), B'(4, 5),
C'(3, 1) |
|
|
|
3.
|
Rotate 270° counterclockwise about the origin. 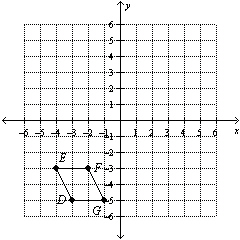 a. | D'(–5, 3), E'(–3, 4), F'(–3,
2), G'(–5, 1) | b. | D'(5, –3), E'(3,
–4), F'(3, –2), G'(5, –1) | c. | D'(3,
5), E'(4, 3), F'(2, 3), G'(1, 5) | d. | D'(5,
3), E'(3, 4), F'(3, 2), G'(5, 1) |
|
|
|
4.
|
Rotate 90° counterclockwise about the origin. 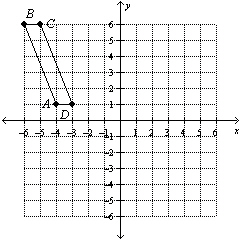 a. | A'(–1, –4), B'(–6, –6),
C'(–6, –5), D'(–1, –3) | b. | A'(4,
1), B'(6, 6), C'(5, 6), D'(3, 1) | c. | A'(1,
4), B'(6, 6), C'(6, 5), D'(1, 3) | d. | A'(–1, 4), B'(–6, 6), C'(–6,
5), D'(–1, 3) |
|
|
|
5.
|
Dilate with a scale factor of 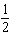 . 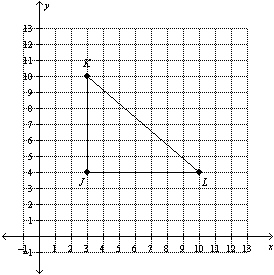 a. | J'(6, 4), K'(6, 10), L'(20, 4) | c. | J'(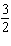 , , 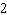 ), K'( ), K'(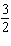 , , 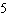 ),
L'( ),
L'(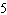 , , 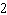 ) ) | b. | J'(6,
8), K'(6, 20), L'(20, 8) | d. | J'(3, 4), K'(3, 10),
L'(10, 4) |
|
|
|
Find the coordinates of the figure after reflecting in the
x-axis.
|
|
|
6.
|
B(1, –1), C(5, –3), D(8, –7), E(3,
–8)
a. | B'(–1, 1), C'(–5, 3), D'(–8,
7), E'(–3, 8) | b. | B'(1, 1), C'(5, 3),
D'(8, 7), E'(3, 8) | c. | B'(–1, –1),
C'(–5, –3), D'(–8, –7), E'(–3,
–8) | d. | B'(1, –1), C'(5, –3), D'(8,
–7), E'(3, –8) |
|
|
|
Find the coordinates of the figure after reflecting in the
y-axis.
|
|
|
7.
|
G(1, –4), H(6, –2), J(5, –6), K(3,
–5)
a. | G'(1, –4), H'(6, –2), J'(5,
–6), K'(3, –5) | b. | G'(–1, 4),
H'(–6, 2), J'(–5, 6), K'(–3,
5) | c. | G'(–1, –4), H'(–6, –2),
J'(–5, –6), K'(–3, –5) | d. | G'(1,
4), H'(6, 2), J'(5, 6), K'(3, 5) |
|
|
|
The vertices of a parallelogram are D(–5, 3), E(–7,
6), F(–3, 6), and G(–1, 3). Rotate the parallelogram as described. Find the
coordinates of the image.
|
|
|
8.
|
270° clockwise about the origin
a. | D'(–3, 5), E'(–6, 7), F'(–6,
3), G'(–3, 1) | b. | D'(–3, –5),
E'(–6, –7), F'(–6, –3), G'(–3,
–1) | c. | D'(3, 5), E'(6, 7), F'(6, 3), G'(3,
1) | d. | D'(–5, –3), E'(–7, –6),
F'(–3, –6), G'(–1,
–3) |
|
|
|
The polygons are similar. Find x.
|
|
|
9.
|
The ratio of the perimeters is 18:9. 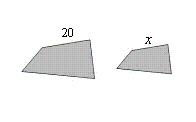
|
|
|
10.
|
|
|
|
11.
|
|
|
|
12.
|
|
Other
|
|
|
1.
|
Extended Response The polygons are congruent. 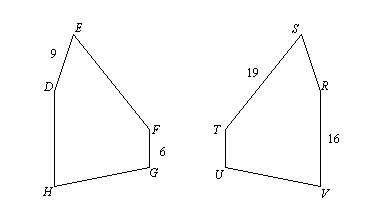 a. What is the length of Side RS?
b. Which
angle of RSTUV corresponds to ÐF?
c.
Side GH is congruent to Side HD. What is the length of Side
GH?
d. What is the perimeter of DEFGH?
|